|
Main
Home
About Me
Guest-Globe
Links
Site Stats
Photos
Kit Car
Index
Geek Stuff
Hardware
Software
3D Scanning
Code Wars
Java
Visuals
R2 Vis
R4 Vis
Tutorials
Feedback
Forum
Contact Me

|  |
|
Fractals are a very interesting phenomena, most are infinitely complex,
meaning the more you zoom in, the more detail there is waiting for you.
Hopefully, I can explain how you make some fractals here...
Nearly all Fractals are made by a process of iteration, and this is where the
link between them and chaos theory comes into play. Basically, you can't write
a complete formula for a chaotic system, instead you have to simulate it, doing one step
at a time (iteration). Iteration is basically taking the output from a formula, and putting
it back into the formula again and again. e.g. If I used Y=2X, and started off
with x as 1, I'd get the following series:
y = 2x = 2
y = 2x = 4
y = 2x = 8
y = 2x = 16
y = 2x = 32

|
Probably the easiest kind of fractal to make is the sierpinski gasket. It works
on some very simple rules. First, you have 3 points, each one is the corner of an
equilateral triangle. You then have a point (I'll call it A) which you can put anywhere in the triangle,
but the middle's probably the best place to start.
Then you just select a point at random, and move A halfway between A's old position
and that of the corner you selected. Then you just leave a dot on the screen, do it a hell
of a lot of times, and you get the picture to the left (The colour of the dots were
the distance the point had to move each time).
The source for the program is below, just type it in in Turbo Pascal:
|
uses crt,dos;
const
GasketSide=3; {Amount of sides (3=triangle)
Odd numbers seem to work, even one's just fill
up the shape}
var x,y,r,c:integer;
a:array [1..GasketSide,0..1] of integer;
{Stores the X and Y Co-ordinates of the edges of the shape}
Begin
randomize; {Create a new set of random numbers}
Writeln('Creating Lookup...');
for r:=1 to GasketSide do
{This fills up the array, it uses Sin and Cos to produce points on a circe}
Begin
a[r,0]:=160+round(95*sin(r*2*pi/GasketSide));
a[r,1]:=100-round(95*cos(r*2*pi/GasketSide));
End;
Writeln('Init Variables...');
x:=160; {Where the point starts off... The middle of the screen}
y:=100;
asm {Initialise screen in 320x200 mode}
mov ax,13h
int 10h
end;
port[$3c8]:=0; {Set up the video palette}
port[$3c9]:=0; {Color 0 = black}
port[$3c9]:=0;
port[$3c9]:=0;
for r:=1 to 255 do {Colors 1-255 blend from blue to red}
Begin
port[$3c9]:=r div 4;
port[$3c9]:=0;
port[$3c9]:=63-(r div 4);
End;
repeat
r:=random(GasketSide)+1; {Guess which corner to move to}
c:=round(sqrt(sqr(abs(a[r,0]-x))+sqr(abs(a[r,1]-y)))*128 / 95);
{The line above figures out a colour using pythagoras,
although you could just replace the whole lot by c:=1; if you only
wanted a blue fractal}
x:=(a[r,0]+x) div 2; {Move half-way between present point and shape corner}
y:=(a[r,1]+y) div 2;
mem[$A000:word(x)+(word(y)*320)]:=c; {Put the point onto the screen}
until keypressed; {Keep adding to it until a key is pressed}
readkey;
textmode(lastmode); {Go back into text mode}
End.
|
Another Interesting point is that a fractal can be created that looks exactly the same
using just pascal's triangle. This is where a triangle is made, where each point is
the sum of the two points above. If you make even numbers black, and odd ones white,
you get the same triangle. Source is below, just put it in Turbo Pascal and to should run.
uses crt,dos;
var a:array [0..127,0..127] of byte; {Array which will have pascal's triangle in}
x,y,c,d:integer;
Begin
for x:=0 to 127 do {Clear our array of values}
for y:=0 to 127 do
a[x,y]:=0;
a[0,0]:=1; {Make top number 1}
for y:=1 to 127 do {Scan down pascal triangle}
for x:=0 to y do
Begin
c:=x; {Get point above-right}
if c<0 then c:=0 else c:=a[c,y-1];
d:=x-1; {Get point above-left}
if d<0 then d:=0 else d:=a[d,y-1];
a[x,y]:=c+d; {Add them together and put in the next row}
End;
asm {Go into graphics mode}
mov ax,13h
int 10h
end;
for x:=0 to 127 do {Plot onto the screen}
for y:=0 to 127 do
mem[$A000:(x+160-(y div 2))+(y*320)]:=(a[x,y] mod 2)*15;
{The (x mod 2)*15 makes odd numbers white, and even numbers
black.}
readkey;
textmode(lastmode); {Go back to text mode}
End.
|
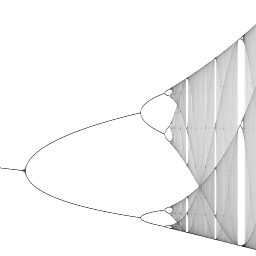
|
This is one of the classical fractals, and works completely by iteration of
a very simple formula. The formula used is y=ax(1-x) or y=ax-ax^2
which is a very simple quadratic formula. Basically, you feed y back into the
formula afterwards as x. A simple way to show this is on a graph of the formula,
where a line (y=x) is drawn. You can then draw lines around, tracing points:
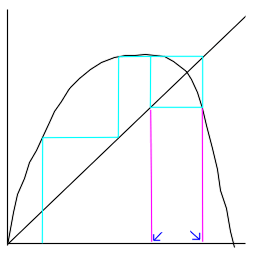 Above, the cyan line is what has been drawn, and you can see that you'd just keep
going around in circles. The purple lines show the 2 points as which it will always
stay.
Above, the cyan line is what has been drawn, and you can see that you'd just keep
going around in circles. The purple lines show the 2 points as which it will always
stay.
So. How do we get a fractal out of this? Well, it turns out that as you vary the
value of A, the points at which the equation 'rests' are different: sometimes it
just stays at one point, sometimes it stays at 2, and sometimes is goes all over
the bloody place.
To graph it, I set the start value for x at 0.2, and then, by varying the value
of A, different points can be found. In the program, x is set at 0.2, then
I feed it through the equation 100 times to make sure it has settled down
into a loop. After this, I go through the loop an extra few hundred times, but
after every time, I put a dot on the screen. The X co-ordinate is A, and the Y
co-ordinate is the new value of x that has been found.
Pascal source code is below:
|
uses crt,dos;
var XVal,A:double;
x,y,i:integer;
w,c:word;
Procedure Iterate;
Begin {Do the formula X = ax(1-x)}
XVal:=A*XVal*(1-XVal);
End;
Begin
asm { Go into graphics mode, 320x200 dots }
mov ax,13h
int 10h
end;
port[$3c8]:=0; {Set the colour palette to go from black to white}
for i:=0 to 255 do
Begin
port[$3c9]:=i div 4;
port[$3c9]:=i div 4;
port[$3c9]:=i div 4;
End;
for x:=0 to 319*8 do {Scan through the lines on the screen (320),
but it is done 8x per line in a different position, to make it
look smoother}
Begin
XVal:=0.2; {Set Starting X value to 0.2}
A:=2.9+(x/(320*8)); {Find value for A, it only really works around
3 and 4, so thats the only range of values we do}
for i:=0 to 100 do {Calculate a few times, to get it to settle down}
Iterate;
for i:=0 to 511 do {Now plot points on the screen}
Begin
Iterate; {Go to next point}
Y:=round(XVal*200); {Calculate position on screen (always between 0 and 1)}
if (y>=0) and (y<=199) then { Check it is actually between 0 and 1 :) }
Begin
w:=(x div 8)+(y*320); {Work out where on the screen memory we must look}
c:=mem[$A000:w]; {Get colour}
inc(c,1); {Make slightly whiter}
if c>255 then c:=255; {Make sure it hasn't gone past white back to black again}
mem[$A000:w]:=c; {Write out to screen}
End;
End;
End;
readkey; {Wait for a keypress}
textmode(lastmode); {Go back to text mode}
end.
|

|
Now for the big one! The mandelbrot.
This actually seems quite simple... It is iterations again, using the formula
Y=X² + C. You set X to zero, then set up C according to where you are on the
page (more of that later). You just iterate until the size of X is greater than 2,
and the colour depends on the amount of iterations you had to do.
But unfortunately there's a catch, the values of X and C
aren't proper numbers. Infact they're complex numbers. Time for a detour:
Whats the square root of -1? Well, As you probably know, there isn't really one.
But, to solve a lot of annoying problems, mathematicians made one, called i.
i is actaully the square root of -1, so i*i=-1. Now, you can't
actually combine a number with i in and a normal number, so they call it
a complex number, and you have to write it as 2 parts e.g. 13 + 24i.
This is how the mandelbrot is created, the complex number is a way to make
it in 2 dimensions, because you can store 2 numbers in one. But, how do you
add complex numbers? Well, thats real easy, say we have X, and Y. X is A+Bi,
and Y is C+Di. So X+Y is A+C+Bi+Di = (A+C) + (B+D)i.
Multiplying is a bit more difficult though. Infact, its just bloody nasty. Now,
I'm guessing you've done quadratic equations, and how to expand brackets, so
if you have (a+b)(c+d) you first multiply the last bracket be a, then
by b, and add them together, so you get: a(c+d) + b(c+d) = ac+ad+bc+bd. In a complex number,
thats what you do as well: (a+bi)(c+di) = a(c+di) + bi(c+di) = ac+adi+bci+bdi² But,
i is the square root of -1, so square it, and you get -1. This means the
formula can be simplified a bit : ac-bd+(ad+bc)i.
Well, thats how to do math with complex numbers, so how does this relate to
Mandelbrot? Well, you set C up in the formula y = x² + C so that
the 'real' bit of the number is the X co-ordinate, and the 'imaginary' (i)
bit is the Y co-ordinate. These are usually between -2 and 2.
Unfortunately, we need all this maths 'cos most programming languages don't
cope with complex numbers, and we have to treat them as seperate variables. If I say
that X is made of A + Bi, Y is made of F + Gi and that C is made of
D + Ei, then via algebra we can say that:
F = A² - B² + D
G = 2AB + E
This is basically our formula sorted, but what about that bit about finding the
size of X? How do you cope with finding the size of a 2D variable. Well, it turns
out you can use pythagoras... If you have a right-angle triangle with sides X,Y
and hypotenuse H, pythagoras says that X² + Y² = H². We just
use X as our real part, Y as our imaginary part, and H is whats left. So..
F²+G²<2² F²+G²<4
And now all thats needed is to write some code to show it:
|
uses crt,dos;
const
ScrX=320; {Screen width and height}
ScrY=200;
X1 = -2; {Position to draw from in fractal}
Y1 = -2;
X2 = 2;
Y2 = 2;
{ Use the values below instead, this gives a zoomed in picture
X1 = 0.3;
Y1 = 0.3;
X2 = 0.5;
Y2 = 0.5;
}
Procedure PutPixel(x,y,col:word);
{ Puts a pixel on a 320x200 VGA screen }
Begin
mem[$A000:x+(y*320)]:=col;
End;
var x,y:integer;
Xr,Xi,Cr,Ci,Temp:double; {X and C}
{ - in two parts because of complex numbers}
iterations:integer;
begin
asm {Go to graphics mode}
mov ax,13h
int 10h
end;
for y:=0 to ScrY-1 do {Scan down screen}
for x:=0 to ScrX-1 do
Begin
Xr:=0; {Set X to zero}
Xi:=0;
Cr:=X1+((X2-X1)*x/ScrX); { Set C up according to screen X and Y coordinates }
Ci:=Y1+((Y2-Y1)*y/ScrY); { And area set to zoom in on }
iterations:=0; {Amount of iterations zeroed}
while (iterations<256) and (sqr(Xr)+Sqr(Xi)<4) do
{ Check size of X<2 - using pythagoras,}
{ this is Xr^2+Xi^2 < 2^2 }
{ If iterations>=255 then we assume its never gonna get
to be equal to 2}
Begin
{ Now calculate X*X + C ... }
Temp:=sqr(Xr)-sqr(Xi)+Cr; {Calculate real part of X}
Xi:=2*Xr*Xi+Ci; {Calculate imaginary part of X}
Xr:=Temp; {Done so the Xi answer is to affected}
inc(iterations); {Add to iteration count}
End;
PutPixel(x,y,iterations and $F);
{Write to screen. 'and $F' keeps the colours in the first 16}
End;
readkey; {Wait for a keypress}
textmode(lastmode); {Go to text mode}
end.
|

|
The plasma shown on the left is not quite as interesting as the mandelbrot, nor
is it actually a fractal, but I'll explain how its done anyway...
Basically, you start off with a rectangle, the 4 corners of which have pixels you
know the colour of, then in the midpoint of each side of the rectangle you have,
put a pixel, whose colour is an average of the two colours on either side of the
bisected line, plus a random number.
Once every side has a colour in the middle of it, put a pixel right in the middle
of the rectangle, using the same idea as before, but with the 4 pixels on the
corners of the rectangle, plus a random number.
You can then divide the rectangle into 4 smaller rectangles, and call yourself
again for each of them. Of course you have to stop when the rectangles get one
pixel large, or you'll keep going on forever... It probably doesn't make too
much sense the way I explained it, so its probably easier to follow the source:
|
uses crt,dos;
Function GetPixel(x,y:word):byte;
Begin
GetPixel:=mem[$A000:X+(Y*320)];
End;
Procedure PutPixel(x,y:word;col:byte);
Begin
mem[$A000:X+(Y*320)]:=col;
End;
Procedure SubDivide(x1,y1,x2,y2:integer);
var midx,midy,dist,hdist:word;
c1,c2,c3,c4:word; {Colours}
Begin
if (x2-x1<2) and (y2-y1<2) then exit;
{If this is pointing at just on pixel, exit because
it doesn't need doing}
dist:=(x2-x1+y2-y1); {Find distance between points.
Use when generating a random number}
hdist:=dist div 2;
midx:=(x1+x2) div 2; {Find Middle Point}
midy:=(y1+y2) div 2;
c1:=GetPixel(x1,y1); {Get pixel colors of corners}
c2:=GetPixel(x2,y1);
c3:=GetPixel(x2,y2);
c4:=GetPixel(x1,y2);
{ If not already defined, work out the midpoints of the corners of
the rectangle by means of an average plus a random number. }
if GetPixel(midx,y1)=0 then PutPixel(midx,y1,(c1+c2+random(dist)-hdist) div 2);
if GetPixel(midx,y2)=0 then PutPixel(midx,y2,(c4+c3+random(dist)-hdist) div 2);
if GetPixel(x1,midy)=0 then PutPixel(x1,midy,(c1+c4+random(dist)-hdist) div 2);
if GetPixel(x2,midy)=0 then PutPixel(x2,midy,(c2+c3+random(dist)-hdist) div 2);
{ Work out the middle point... }
putpixel(midx,midy,(c1+c2+c3+c4+random(dist)-hdist) div 4);
{ Now divide this rectangle into 4, and call again for each smaller
rectangle }
SubDivide(x1,y1,midx,midy);
SubDivide(midx,y1,x2,midy);
SubDivide(x1,midy,midx,y2);
SubDivide(midx,midy,x2,y2);
End;
var i:integer;
Begin
randomize; {Initialise random number generator}
asm { Put into 320x200 video mode }
mov ax,13h
int 10h
end;
port[$3c8]:=0; {Change the colour palette}
for i:=0 to 255 do
Begin
if i<128 then
Begin
port[$3c9]:=63-(i div 2);
port[$3c9]:=i div 2;
port[$3c9]:=0;
End else
Begin
port[$3c9]:=0;
port[$3c9]:=63-((i-128) div 2);
port[$3c9]:=(i-128) div 2;
End;
End;
PutPixel(0,0,128); {Set up the 4 corners of the screen}
PutPixel(319,0,128);
PutPixel(319,199,128);
PutPixel(0,199,128);
subdivide(0,0,319,199); {Call the recursive plasma routine}
readkey; {Wait for a keypress}
textmode(lastmode); {Return to text mode}
End.
|
In Pascal, the real variable is usually used for floating point calculations,
but this is not supported by the computer's Floating Point Unit, so it has to do it
by hand. Using the double variable instead of real will dramatically
improve performance...
|





